МБОУ «Краснокосаровская СОШ».Мглинского района, Брянской области
«Арифметический квадратный корень»
Подготовила: учитель
математики Зайцева Т.П.
Технология критического мышления
Тип урока: урок введения нового материала.
Вид урока: урок-практикум.
Цель урока: рассмотреть понятие арифметического квадратного корня
Задачи урока:
Учебная: повторить формулы сокращенного умножения (разность квадратов); ввести понятие арифметического квадратного корня, определить условия применимости, обозначение; научиться вычислять и применять при решении задач
Развивающая: развивать логическое мышление, память, внимание, навыки самостоятельной и творческой работы, математической речи, контроля и самоконтроля; формировать информационную, когнитивную, коммуникативную компетенции;
Воспитательная: воспитывать интерес к предмету, точность и аккуратность в оформлении решений.
План урока:
1. Определение целей урока
2.Вводное повторение
3. Введение определения, обозначения.
4. Рефлексия.
5. Подведение итогов.
Использование доски
|
Основное свойство квадратного корня |
Тема урока |
Пример 1 |
Ход урока
1. Определение целей урока
Приветственное слово учителя. Введение целей урока(цели урока обучающиеся класса определяют сами после объявления темы урока).
2.Вводное повторение
Мозговой штурм: Работа в группах
Вычислите:32=9;102=100;122=144;132=169;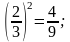
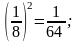 0,12=0,01; 0,132=0,0169.
0,12=0,01; 0,132=0,0169.
Разложите на множители: (у2-81)=(у-9)(у+9); (а2-144)=(а-12)(а+12).
Площадь квадратного участка земли равна 144 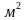 . Найдите его сторону.
. Найдите его сторону.
3. Введение определения, обозначения.
Рассмотрим два уравнения х2=4 и х2=9. Решим с помощью формул сокращенного умножения. Но для уравнения х2=5 таким же способом пока мы решить не можем. Встретившись впервые с подобной ситуацией, математики поняли, что надо придумать способ ее описания на математическом языке. Они ввели в рассмотрение новый символ и с его помощью корни уравнения х2 = 5 записали так: х1=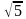 , х2 = –
, х2 = –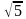 .
.
УЧЕБНИК стр.45 Определение. Квадратным корнем из неотрицательного числа а называют такое неотрицательное число, квадрат которого равен а.
А теперь давайте рассмотрим таблицу на стр.46
Какие две операции показаны в ней? Обратите внимание на операцию извлечения корня из числа.
Иногда говорят не «квадратный корень», а «арифметический квадратный корень». Термин «арифметический» мы опускаем для краткости.
НА ДОСКЕ. Вычислите:
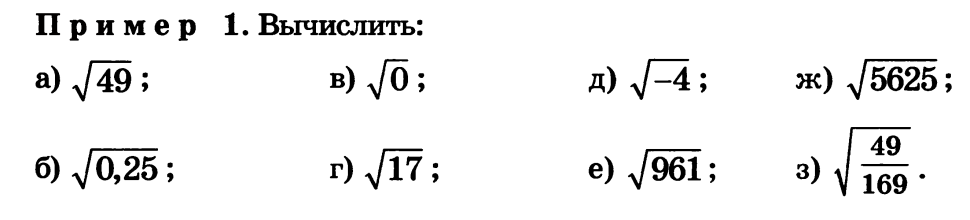
Праздник квадратного корня
Впервые этот праздник отмечался 9 сентября 1981 года (09-09-81). Основателем праздника является школьный учитель Рон Гордон (RonGordon) из города Редвуд Сити, Калифорния, США.
Главным блюдом на этом «праздничном столе» обычно являются вареные кубики из корнеплодов и выпечка в форме математического знака квадратного корня
4. Рефлексия
ЗАДАЧНИК стр.57 пункт.10
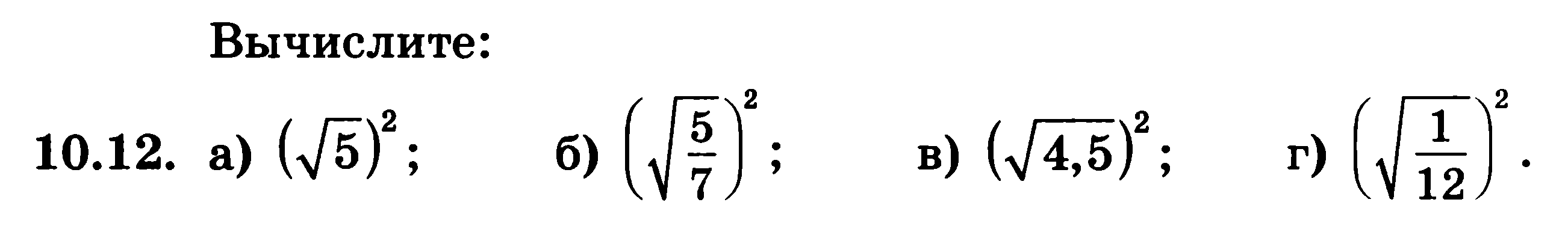
На доске и в тетрадях №20(в,г),23(а,б)
![]()
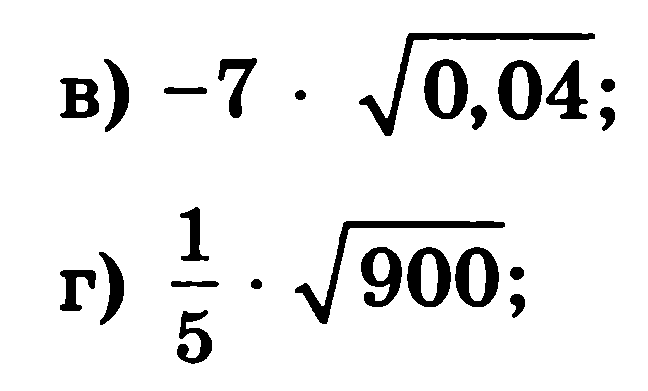
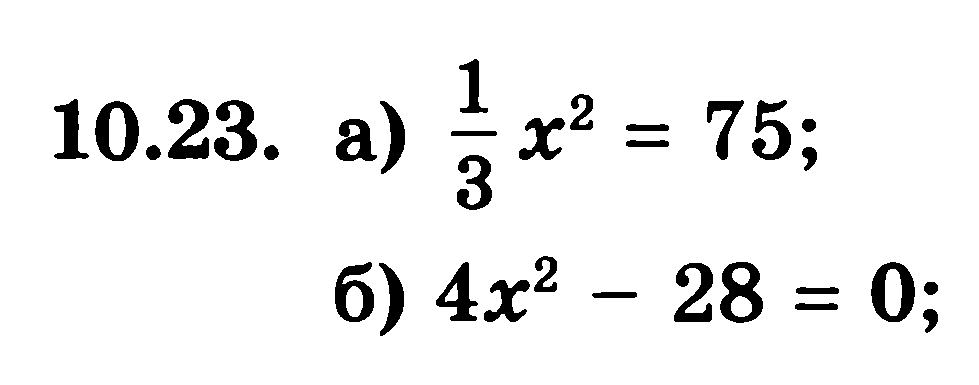
Самостоятельная работа
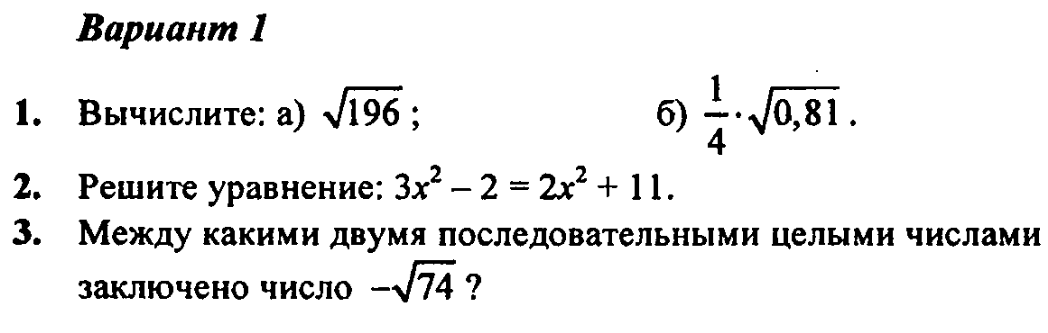
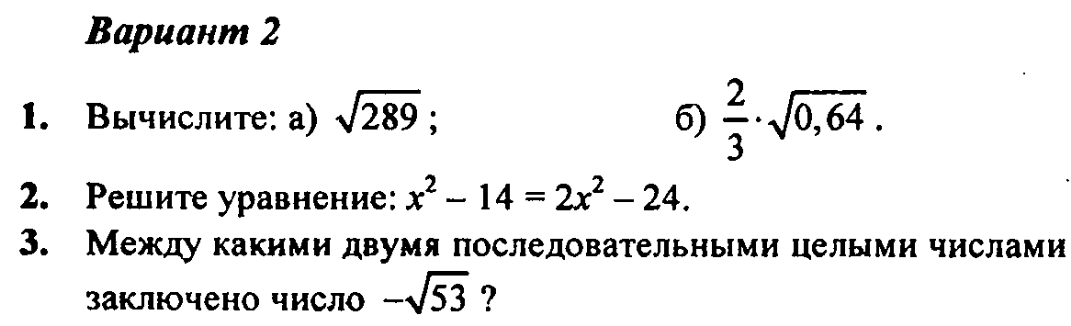
Индивидуальные задания
|
№ |
Вопрос |
Да |
Нет |
Обозначение |
Пример |
|
1 |
Знаю ли я, что такое квадратный корень? |
|
|
|
|
|
2 |
Знаю ли основное свойство арифметического квадратного корня? |
|
|
|
|
|
3 |
Смогу ли я найти квадратный корень числа? |
|
|
|
|
5. Подведение итогов.
Что мы сегодня изучили?
Что называют арифметическим квадратным корнем?
Когда имеет смысл выражение 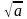 ?
?
Д/З п.10 изуч, ![]() устно,№
устно,№![]()
![]()