Устный счет
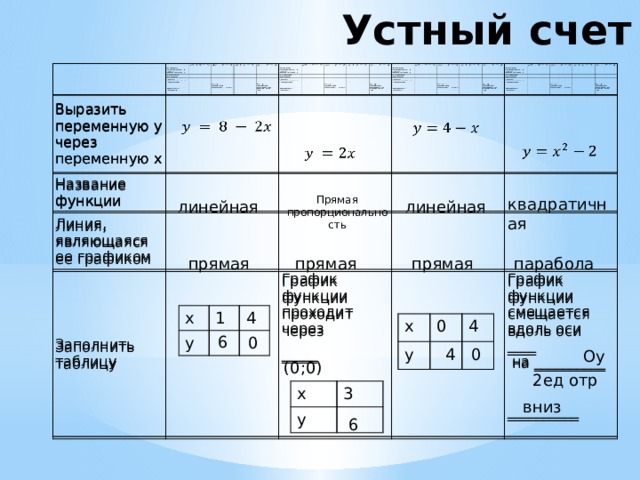
Выразить переменную y через переменную x
Выразить переменную y через переменную x
Название функции
Название функции
Линия, являющаяся ее графиком
Линия, являющаяся ее графиком
Заполнить таблицу
Заполнить таблицу
График функции проходит через
График функции проходит через
График функции смещается вдоль оси ____
_____
График функции смещается вдоль оси ____
_____
на __________
на __________
__________
__________
Прямая пропорциональность
квадратичная
линейная
линейная
прямая
прямая
парабола
прямая
x
y
1
4
x
y
0
4
6
0
4
0
Oy
(0;0)
2ед отр
x
y
3
вниз
6

Решите системы уравнений
1) 2)

«Решение систем, составленных из двух уравнений второй или одного уравнения первой, и другого второй степени»

Графический способ
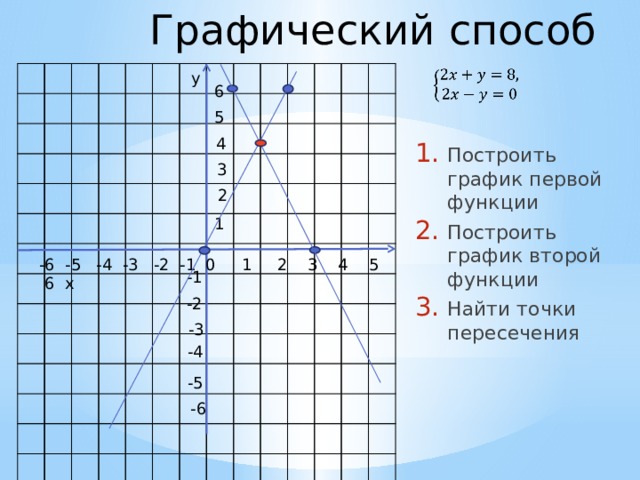
Графический способ
y
6
5
4
- Построить график первой функции
- Построить график второй функции
- Найти точки пересечения
3
2
1
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x
-1
-2
-3
-4
-5
-6

Способ сложения
- Если требуется, уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.
- Складывая полученные уравнения
- Решить полученное уравнение с одним неизвестным и найти одну из переменных.
- Подставить полученное значение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.
Ответ: (2;4)

Способ подстановки
- Выбрать одно уравнение (лучше выбирать то, где числа меньше) и выразить из него одну переменную через другую, например, x через y. (можно и y через x).
- Полученное выражение подставить вместо соответствующей переменной в другое уравнение. Таким образом, у нас получится уравнение с одной неизвестной.
- Решаем полученное уравнение и получаем значение одной переменной.
- Подставляем полученное значение в выражение, полученное в первом пункте, получаем вторую неизвестную из решения.
Ответ: (2;4)

Решите системы уравнений
1) 2)
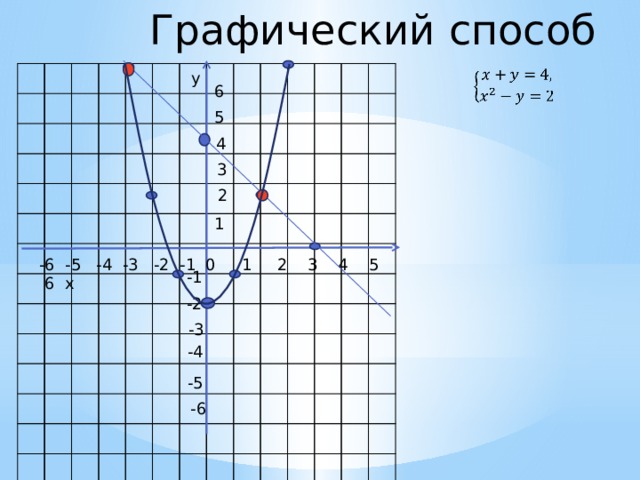
Графический способ
y
6
5
4
3
2
1
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x
-1
-2
-3
-4
-5
-6

Домашнее задание
- повторить алгоритмы,
- ответить на вопрос « Всегда ли все три способа подходят для решения систем уравнений? »
- Решить систему