Если ты услышишь, что кто-то не любит математику, не верь.
Её нельзя не любить — её возможно только не знать
.
- Великий китайский педагог Конфуций , который жил более 2400 лет тому назад сказал примерно так:
- То, что я слышу , я забываю.
- То, что вижу и слышу, я немного помню.
- Когда я слышу, вижу, обсуждаю и делаю, я запоминаю.
- Когда я передаю знания другим, я учусь.
- обобщение и систематизация знаний, умений и навыков, отработка основных алгоритмов в коллективной работе по решению различных неравенств.
I – Линейное неравенство
- Разминка:
- выполни действия
- найди ошибку
- заполни таблицу
- Объясни другу: повторение свойств и алгоритмов.
- Один за всех и все за одного — решение линейных неравенств:
- работа у доски
- работа в группе
- Каждый сам за себя – самостоятельная работа с самопроверкой
I I– Квадратное неравенство
- Объясни другу:
- алгоритм решения квадратного уравнения (через дискриминант)
- алгоритм решения квадратного уравнения, по теореме обратной т.Виета
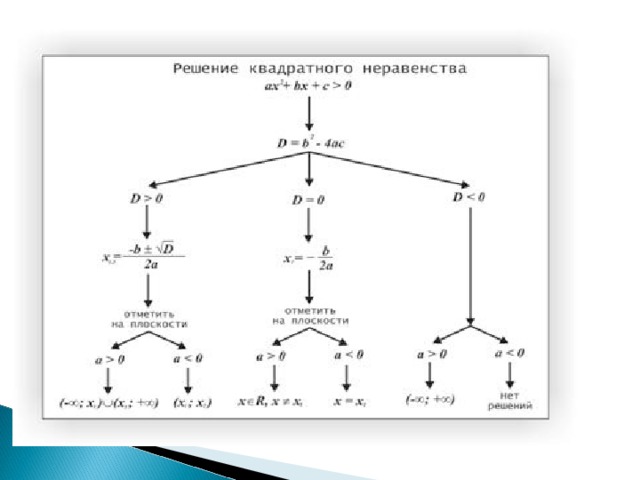
- алгоритм решения квадратного неравенства
- Работа в группе:
- задание на соответствие
- работа по карточке
- Итоговая разноуровневая самостоятельная работа с последующей самопроверкой
- Немного истории…
Изобретение знаков неравенства связывают с именем ученого Г.Гариотта (1560-1621)
- Действия с рациональными числами
- Правила раскрытия скобок
- Приведение подобных слагаемых
- Основные свойства числовых неравенств
- -2,1+3,7- 4,4
Ответы
- — 2,8
- -4,1-(-1,8+2,5)
- 0,2
- — 21,5
- 0,5-12,7- 9,3
- 7(2х-3) +4( 3х-2)
- 14х-21+12х-8=
26х+29
- -8(2-2у) + 4(3-4у)
- -16 -16у +12 – 16у= -32у -4
-х +2 -10-х = -2х -8
- -0,5(-2х+4)-(10-х)
8 х Х ≥ -15 х ≤ 6 6 ≤ х ≤ 18 х 2 7″ width=»640″
Неравенство
Числовой
промежуток
2
-5 ≤ х ≤ -1
(2;7)
Геометрическая интерпретация
х 8
х
Х ≥ -15
х ≤ 6
6 ≤ х ≤ 18
х
2
7
- Раскрой скобки
- Перенеси неизвестные слагаемые в левую часть неравенства, а известные – в правую; при этом не забудь поменять знак слагаемых на противоположный
- Приведи подобные в каждой части неравенства
- Раздели число в правой части на коэффициент при неизвестном; при этом не забудь: если делим на отрицательное число, знак неравенства меняем на противоположный.
- На числовом луче отметь полученное число, укажи интервал
2(5х-7) 9х-3 10х-14 9х-10х 3-14 -х -11 Х Ответ х €(-∞; 11)» width=»640″
- 3(3х-1) 2(5х-7)
- 9х-3 10х-14
- 9х-10х 3-14
- -х -11
- Х
- Ответ х €(-∞; 11)
х
11
12x-1 ( 2б) (3б) (4б) Карточка №1 Вариант 1. -3х ≥ 21 (1б) 3- 4 a 13 (1б) 5( x-1) +7 1-3(x+2) ( 2б) (3 б) (4б)» width=»640″
- Карточка №1
- Вариант 2.
- -2х ≥12 (1б)
- 3-2a
- 17-( x+2) 12x-1 ( 2б)
- (3б)
(4б)
Карточка №1
- Вариант 1.
- -3х ≥ 21 (1б)
- 3- 4 a 13 (1б)
- 5( x-1) +7 1-3(x+2) ( 2б)
- (3 б)
- (4б)
12 ( 1б.) в) 15-x 10-6x ( 1б.) г) 4(x-1)-(9x-5) ≥ 3 ( 2б.) д) 5+x 3x-3(4x+5) ( 2б.) (5 б)» width=»640″
- а) -4x
- б) -6x 12 ( 1б.)
- в) 15-x 10-6x ( 1б.)
- г) 4(x-1)-(9x-5) ≥ 3 ( 2б.)
- д) 5+x 3x-3(4x+5) ( 2б.)
- (5 б)
4 в Xг X -1 д X≤0,4 XОтвет» width=»640″
а
б
Х 4
в
X
г
X -1
д
X≤0,4
X
Ответ
0: 2 корня х 1, 2 = − b ± √ D» width=»640″
- Уметь решать полное квадратное уравнение:
- а х 2 + b х + с = 0
- D = b 2 − 4 ac
- 1 . D 0: 2 корня
х 1, 2 = − b ± √ D
2 a
- 2 . D = 0 : 1 корень х 1 = х 2
- 3 . D
- Применять обратную теорему Виета
- а х 2 + b х + с = 0, а = 1.
- Если х 1 и х 2 − корни уравнения ,
т о х 1 + х 2 = − b
х 1 · х 2 = с ,
Франсуа Виет
французский математик
(1540 -1603)
- Найти корни квадратного трехчлена
а х 2 + b х + с
- Отметить корни на оси х и определить, куда(вверх или вниз) направлены ветви параболы, служащей графиком функции у = а х 2 + b х + с ; сделать набросок графика.
- С помощью полученной геометрической модели определить, на каких промежутках оси х ординаты графика (у) положительны(отрицательны); включить эти промежутки в ответ.
так как выполняется условие
то
— 1
а)
— 1
г)
— 1
б)
— 1
— 1
д)
в)
- 1) г)
- 2) а)
- 3) б)
- 4) в)
- 5) д)
0 (1б) 2 .х 2 +2х – 3 ≤ 0 (2б) 3. -х² +2х-1 ≥0. (2б) 4. 3х 2 +5х- 2 0 (3б) Карточка №2″ width=»640″
Карточка №2
- Вариант 2.
1. (х – 3)(х – 5) 0 (1б)
2 .х 2 +2х – 3 ≤ 0 (2б)
3. -х² +2х-1 ≥0. (2б)
4. 3х 2 +5х- 2 0 (3б)
Карточка №2
- Вариант 1
- 1. (х – 4)(х – 2)
- 2. х 2 +2х — 3 0 (2б)
- 3. — х² +2х-1 ≤0, (2б)
- 4. 2х² — 9х +10
I уровень II уровень
- 11х – 2
- 2 – 3у ≥ -4 (1б) 4 (а +
– 7(а — 1)
- 17 – х ≤ 11 (1б) 4(в – 1,5) – 1,2 ≥ 6в – 1 (2б)
- Х² — 64 0 (3б)
- ( х+8)(х-3) ≥0 (1б) 4х² + 3х -10
I уровень II уровень
- Х
- У ≤ -3 а 9
- Х ≥ 6 в ≤ — 3,1
- (-8 ;8) (-1,5; 6,5)
- (-∞;-8 ]v[3 ;∞) (-1,25; 0,5)
- Карточка №1
- Самостоят. работа №1
- 2 — 4б =«3»
- 5 -7б =«4»
- 8-11б =«5»
- 2 — 4б =«3»
- 5 -7б =«4»
- 8-12б =«5»
- Карточка №2
- Самостоят. работа №2
- 1-2б =«3»
- 3-5б =«4»
- 6-8б =«5»
- 2 — 4б =«3»
- 5 -7б =«4»
- 8-12б =«5»
Человек не знающий математики, не способен ни к каким другим наукам. Более того, он даже не способен оценить уровень своего невежества.»
Роджер Бэкон. (1214-1294г)
