Урок по теме « Применение основных тригонометрических тождеств к преобразованию выражений»
9 класс
Цель:
-
повторить изученный ранее материал, рассмотреть применение основных тригонометрических тождеств к упрощению тригонометрических выражений и доказательству тождеств;
-
развивать внимательность, логическое мышление, познавательную активность, математическую речь;
-
воспитывать сознательное отношение к усвоению учебного материала, настойчивость, самостоятельность мышления.
Тип урока – комбинированный.
Психологический настрой.
— Здравствуйте, ребята! Я рада вас видеть и очень хочу начать работу с вами! Хорошего вам настроения и успехов!
1 этап. Актуализация прежних знаний.
Устные упражнения.
№1. Какой четверти принадлежит угол, если
-
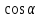
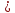 0,
0, 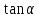
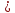 0, 2)
0, 2) 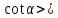 0,
0, 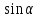
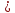 0, 3)
0, 3) 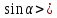 0,
0, 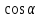
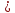 0
0
4)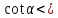 0,
0, 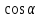
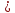 0, 5)
0, 5) 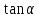
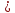 0,
0, 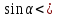 0.
0.
№2. Найдите значение выражения
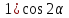 , если α =
, если α = 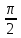 :
:
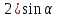 , если α = — 150:
, если α = — 150:
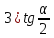 , если α = -2π:
, если α = -2π:
4) 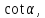 если α = 405
если α = 405
№3 Упростите выражение
-
( 1 – sin2 α ) cos 2α;
-
(1 – cos2 α) sin α;
-
(1 – cos2 α) (1 – sin2 α).
№4. Найдите значение выражения
1) Cos(-810 °);
2) Tg(-60 °)* ctg(-60° ) ;
3) tg30°/ sin30°.
Пока весь класс выполняет устные упражнения, три ученика работают у доски над по карточкам с заданиями разного уровня
Карточка А. Упростите выражения:
-
1 – cos 2α — sin2 α
-
cos α *sin α *tg α.
Карточка В. Известно, что cos α = 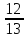 270°
270° 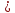 α
α 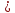 360°. Найти значение остальных тригонометрических функций для этого угла.
360°. Найти значение остальных тригонометрических функций для этого угла.
Карточка С. Найдите значения выражения
(5sin α -2cos α)/ ( 5cos α + sin α) , если tg α = 2.
2 этап. Изучение нового материала
Учитель объявляет цель урока, ученики записывают тему урока в тетрадях.
Цель: научиться упрощать тригонометрические выражения и доказывать тригонометрические тождества.
Открываем учебник на стр112 п20 и самостоятельно прорабатываем тему.
Ответьте на вопросы
Вопрос 1. Как доказываются тригонометрические тождества?
Ответ. Способы доказательства:
-
Преобразуя левую часть тождества, и показываем, что она равна правой части;
-
Преобразуя правую часть тождества, и показываем, что она равна левой части;
-
Преобразуем левую и правую части тождества, и показываем, что они равны одному и тому же выражению.
-
Доказываем, что разность левой и правой частей равна нулю;
-
Доказываем тождество, используя основное свойство пропорции.
Вопрос2. Каким выражением на основе основных тригонометрических выражений можно заменить данные выражения? На доске написаны выражения. Ученики должны подобрать к ним соответствующие выражения, написанные на карточках.
-
cos α2 + sin2 α на 1
-
1 на cos α2 + sin2 α или на tg α *ctg α
-
1 + tg2 α на 1/cos 2α
-
1/sin2 α на 1 + ctg 2α
-
1/cos 2α на 1 + tg2 α
-
sinα/ cosα на tgα
-
ctgα на cosα/sinα
-
cgα на sinα/ cosα
-
tg α *ctg α на 1
-
cos α/ sin α на ctgα
-
1 + ctg2 α на 1/sin2 α
3 этап. Первичное закрепление теоретических выводов при решении упражнений.
№1. Упростите выражения:
-
1 — 1/sin2 α; 2) 1 – (
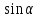 *
* 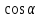 ) / ctg α.
) / ctg α.
№2. Докажите, что для любого α значение выражения (1 + 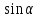 ) /
) / 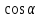 * (1 —
* (1 — 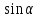 )/ /
)/ /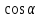 равно 1.
равно 1.
№3. Докажите тождество sin α /(1 – cosα) = ( 1+ cosα )/ sin α
Пока решаем задания всем классом трое ребят работают индивидуально по карточкам разного уровня сложности.
А) Докажите тождество 1/( 1 + tg2 α) + sin2 α = 1.
В) Полагая, что α = 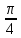 , найдите значение выражения ( sin2 α – 1)/(1 — cos 2α ).
, найдите значение выражения ( sin2 α – 1)/(1 — cos 2α ).
С) упростите выражение (cos 2α — sin2 α)/ (cosα — sin α ) + cosα * sin α .
4этап . Групповая работа. Класс делится на 4 группы по 4 человека( объединяются 2 соседние парты в ряду)
1 группа №319
2 группа №321
3 группа №323
4 группа №325
Затем учащиеся каждой группы представляют решение одного на их взгляд самого интересного задания
5 этап. Задание на дом. П20 проработать № №317, 318, 322. Для желающих дополнительно№324.
6этап. Подведение итогов урока
7.Рефлексия
Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
Использованная литература:
-
Учебник Алгебра 9 класс . А.Абылкасымова, И.Бекбоев, А.Абдиев, З.Жумагулова
Алматы: Издательство «Мектеп» 2015г
-
Дидактические материалы по алгебре 9 класс Ю.Н.Макарычев, Н.Г.Миндюк, Л.М.Короткова.