
Если мы действительно знаем что-то, то мы знаем это благодаря изучению математики .
П.Гассенди

Тема урока: «Преобразование тригонометрических выражений и графиков тригонометрических функций»

Цель урока: закрепить изученный материал в ходе решения задач и построения графиков синуса и косинуса.

Разминка: Кросс-опрос
- 1.Верно ли равенство: SinП =Sin180
- 2.tg0=….
- 3. Верно ли равенство:
- 4.cos 2 α-Sin 2 α=…
- 5. Верно ли равенство:
- 6. cos 2 α+Sin 2 α=…
- 7. Sin0=
- 8. cos0=
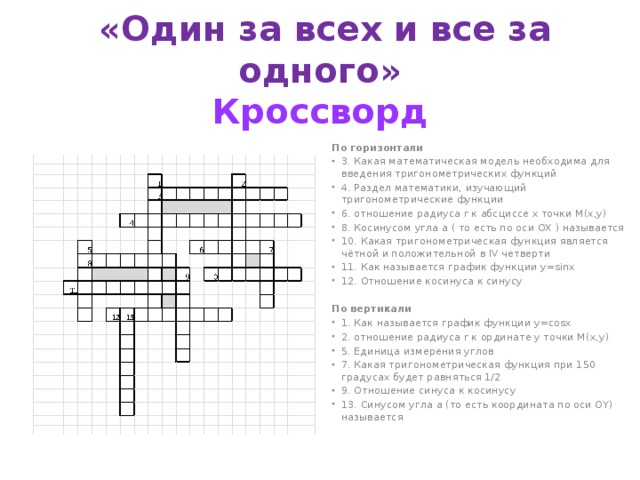
«Один за всех и все за одного» Кроссворд
По горизонтали
- 3. Какая математическая модель необходима для введения тригонометрических функций
- 4. Раздел математики, изучающий тригонометрические функции
- 6. отношение радиуса r к абсциссе x точки M(x,y)
- 8. Косинусом угла a ( то есть по оси OX ) называется
- 10. Какая тригонометрическая функция является чётной и положительной в IV четверти
- 11. Как называется график функции y=sinx
- 12. Отношение косинуса к синусу
По вертикали
- 1. Как называется график функции y=cosx
- 2. отношение радиуса r к ординате y точки M(x,y)
- 5. Единица измерения углов
- 7. Какая тригонометрическая функция при 150 градусах будет равняться 1/2
- 9. Отношение синуса к косинусу
- 13. Синусом угла a (то есть координата по оси OY) называется
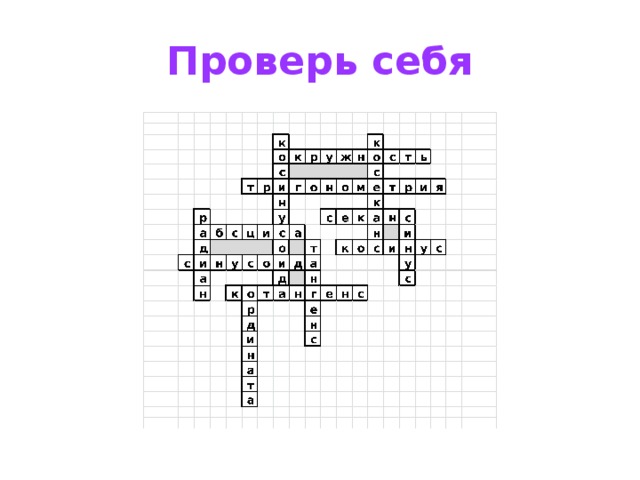
Проверь себя
Все вместе
- Найдите значение Sinα,
если cosα = -0.6 и
0 
История возникновения тригонометрии
Выполнил студент
Группы:С-14/9
Лазарев И.
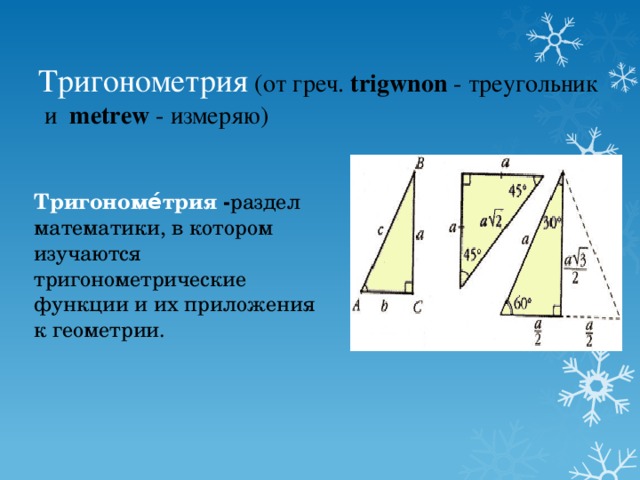
Тригонометрия (от греч. trigwnon — треугольник и metrew — измеряю)
Тригономе́трия — раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.

История
- Тригонометрия возникла из практических нужд человека. С ее помощью можно определить расстояние до недоступных предметов и, вообще существенно упрощать процесс геодезической съемки местности для составления географических карт.
- Возникновение тригонометрии связано с землемерием, астрономией и строительным делом.

Древняя Греция
Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды».

Средневековая Индия
- Другие источники сообщают, что именно замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.

Арабские Зиджи
Улугбек (1394-1449) -основатель научной школы в Самарканде.
Первые трактаты о плоской тригонометрии
(X—XI вв.).

Преобразование тригонометрии в самостоятельную часть математики
Основные сочинения:
Насирэддин Туей — «Трактат о полном четырехстороннике»
- 1-ая и 2-ая книги включают в себя вспомогательный материал для построения тригонометрии;
- в 3-ей книге введены понятия синуса и косинуса, правила решения плоских треугольников и доказательство теоремы синусов;
- в 4-ой и 5-ой книгах показаны основы сферической тригонометрии.
Насирэддин Туей

Иоганн Мюллер ( Региомонтан) –
«Пять книг о треугольниках всех видов»
Коперник — «Об обращениях небесных тел»

Тихо-Браге — разработал много вычислительных приемов, облегчающих задачу решения треугольников
Ретик (1551 г.) – составил таблицы тригонометрических функций, по форме и по составу близкие к ныне употребляемым
Г. С. Клюгель (1770 г.) – ввел понятие
«тригонометрические функции»

Синус
- Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности встречаются уже в III веке до н.э. в работах великих математиков Древней Греции Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия. Современный синус , например, изучался как полухорда, на которую опирается центральный угол величиной , или как хорда удвоенной дуги.

Косинус и тангенс
- Слово косинус намного моложе. Косинус это сокращение латинского выражения completely sinus, т. е. “дополнительный синус”.
- Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов.

Спасибо за внимание!

Тригонометрия в профессии сварщик
Выполнил студент
Группы: С-14/9
Вороненко Евгения

В профессии сварщик очень часто встречается тригонометрия, так как основа профессии- постоянная работа с металлом, который имеет геометрическую форму.
Предположим те же самые трубы для подачи воды, которая поступает к нам в дома, здесь без тригонометрии не
обойтись.
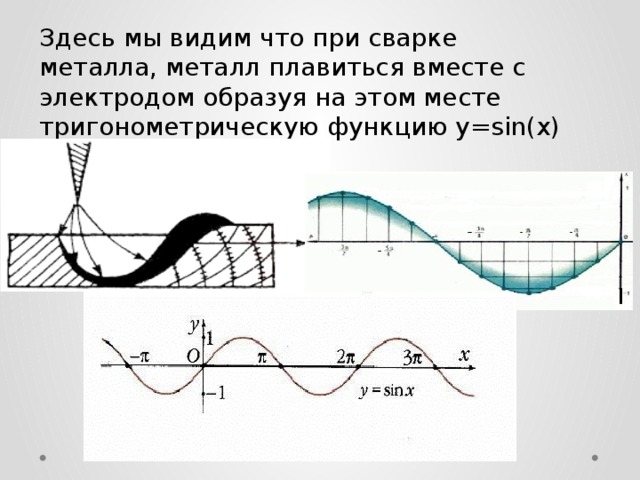
Здесь мы видим что при сварке металла, металл плавиться вместе с электродом образуя на этом месте тригонометрическую функцию y=sin(x)
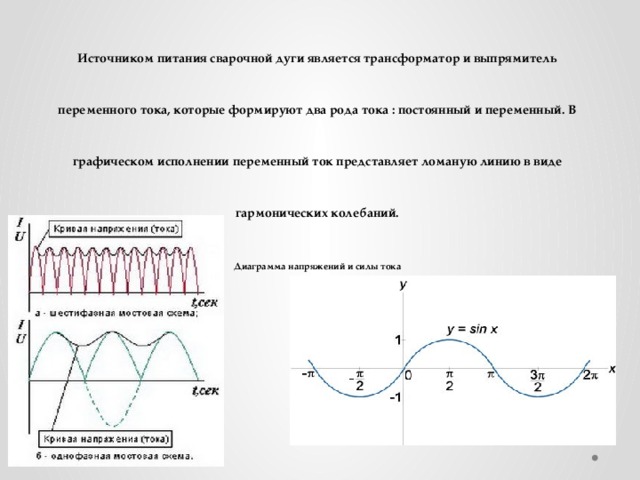
Источником питания сварочной дуги является трансформатор и выпрямитель переменного тока, которые формируют два рода тока : постоянный и переменный. В графическом исполнении переменный ток представляет ломаную линию в виде гармонических колебаний. Диаграмма напряжений и силы тока
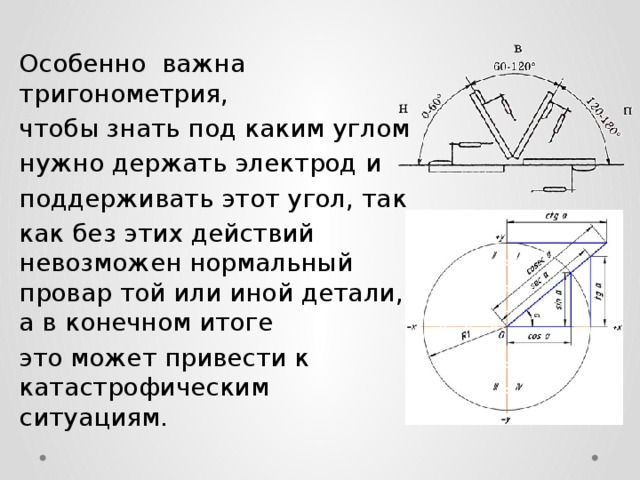
Особенно важна тригонометрия,
чтобы знать под каким углом
нужно держать электрод и
поддерживать этот угол, так
как без этих действий невозможен нормальный провар той или иной детали, а в конечном итоге
это может привести к катастрофическим ситуациям.

В этом случае нужно рассчитывать по формулам: какой диаметр трубы, какой толщины эта труба, выбрать угол наклона электрода, так чтобы предотвратить образование дефектов в этой трубе и т.д.

В конечном итоге я хочу сказать, что без тригонометрии сварка могла и не существовать, а без сварки не было бы: водопровода, заводов, машин и так далее.

Спасибо за внимание.

Тригонометрия в окружающем нас мире и жизни человека
Выполнил студент группы: С-14/9 Павленко Иван

- Тригонометрия — это раздел математики, изучающий тригонометрические функции. Сложно представить, но с этой наукой мы сталкиваемся в нашей повседневной жизни в таких науках, как физика, биология, не последнюю роль она играет и в медицине, и, что самое интересное, без неё не обошлось даже в музыке и архитектуре.

По звёздам вычисляли местонахождение корабля в море.
Древние люди вычисляли высоту дерева, сравнивая длину его тени с длиной тени от шеста, высота которого была известна.

Тригонометрия в физике
В технике и окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными . Колебательные явления различной физической природы подчиняются общим закономерностям.
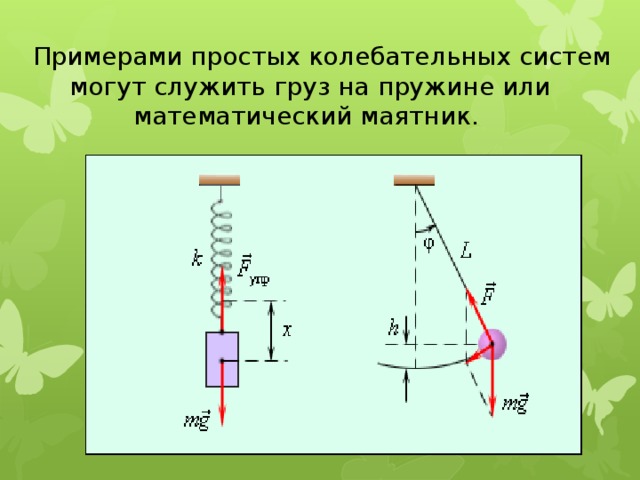
Примерами простых колебательных систем могут служить груз на пружине или математический маятник.
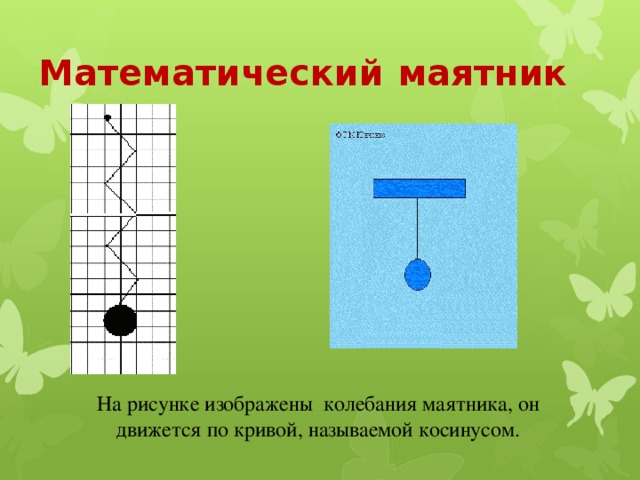
Математический маятник
На рисунке изображены колебания маятника, он движется по кривой, называемой косинусом.
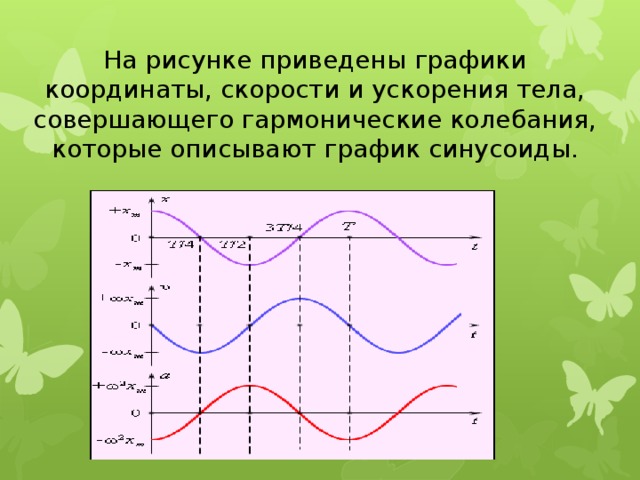
На рисунке приведены графики координаты, скорости и ускорения тела,
совершающего гармонические колебания, которые описывают график синусоиды.
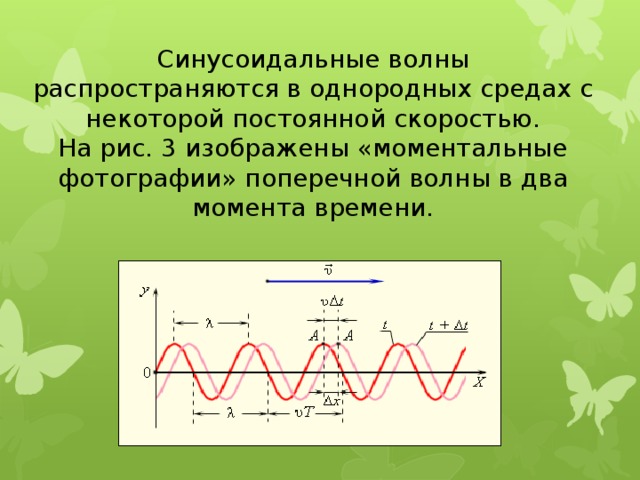
Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью. На рис. 3 изображены «моментальные фотографии» поперечной волны в два момента времени.
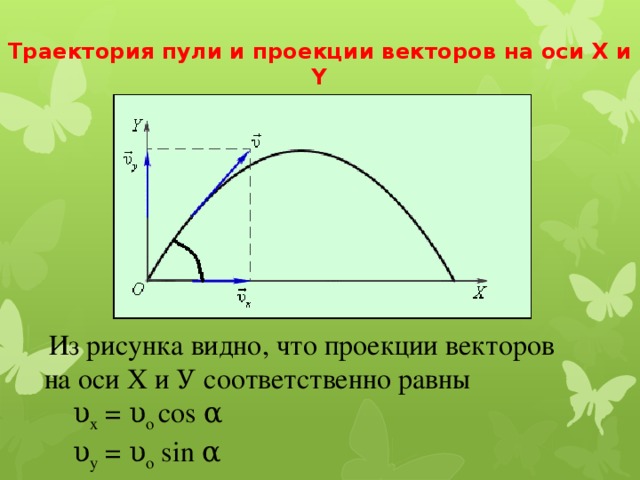
Траектория пули и проекции векторов на оси X и Y
Из рисунка видно, что проекции векторов на оси Х и У соответственно равны
υ x = υ o cos α
υ y = υ o sin α

Радуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления:
n 1 — показатель преломления первой среды n 2 — показатель преломления второй среды
α -угол падения, β -угол преломления света
sin α / sin β = n 1 / n 2
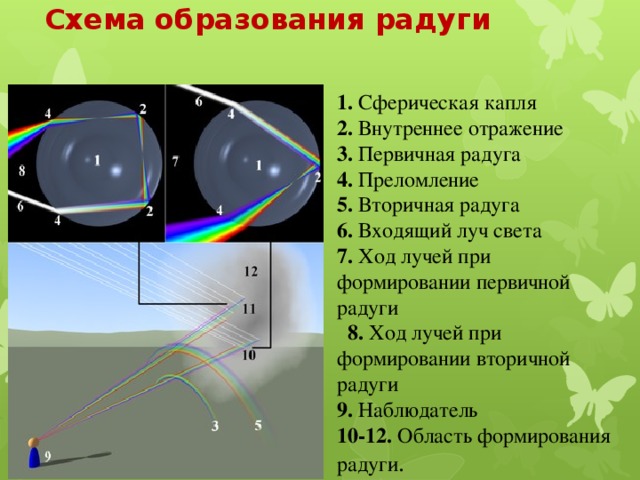
Схема образования радуги
1. Сферическая капля
2. Внутреннее отражение
3. Первичная радуга
4. Преломление 5. Вторичная радуга 6. Входящий луч света 7. Ход лучей при формировании первичной радуги 8. Ход лучей при формировании вторичной радуги 9. Наблюдатель 10-12. Область формирования радуги .

Северное сияние – это п роникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.

Тригонометрия и тригонометрические
функции в медицине и биологии .
- Одно из фундаментальных свойств живой природы — это цикличность большинства происходящих в ней процессов.
- Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
- Модель биоритмов можно построить с помощью тригонометрических функций.
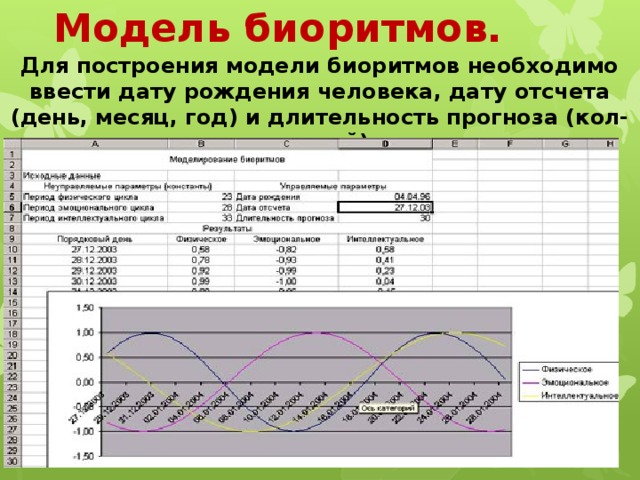
Модель биоритмов.
Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).

Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца — комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.

Тригонометрия в биологии
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.

При полёте птицы, траектория взмаха крыльев образует синусоиду.

Тригонометрия в архитектуре
Детская школа Гауди в Барселоне

Сантьяго Калатрава Винодельня «Бодегас Исиос»

Феликс Кандела Ресторан в Лос-Манантиалесе

Спасибо за внимание!

Я славлю разум человека,
Дела его волшебных рук,
Надежду нынешнего века –
Царицу всех земных наук

Подведение итогов Д/З № 235,236 а)