Тема урока: Решение практических задач на применение подобия треугольников.
Цель урока:
Систематизировать и обобщить знания учащихся по теме «Подобие треугольников»
Формировать умения и навыки применения признаков подобия треугольников и их следствий при решении задач;
Совершенствовать навыки решения практических задач;
Развивать умение обобщать, абстрагировать и конкретизировать свойства выученных объектов и отношений и применять их при решении практических задач;
Воспитывать культуру устной математической речи и познавательного интереса учащихся;
Развивать познавательную творческую деятельность и умение анализировать и преодолевать трудные моменты, возникающие во время решения математических задач;
Реализовать межпредметные связи с алгеброй, физикой, географией, астрономией, историей и литературой;
Способствовать возникновению у учеников интереса к изучению геометрии, осознанию ее красоты и значимости.
Тип урока: систематизация, обобщение и использование на практике знаний, умений и навыков.
Оборудование: компьютер, проектор, разработанная презентация урока в слайдах в программе Power point, карточки с высказываниями Фалеса.
ХОД УРОКА
Организационный момент. Мотивация учебной деятельности.
Учитель сообщает тему и цель урока.
Учитель. Решая различные задачи по теме «Подобие треугольников» мы не задумывались, где и как можно применить полученные знания в жизни. Сегодня на уроке мы убедимся, что ранее полученные знания нужны в жизни, а предмет геометрия – наука, которая тесно связана с жизненными ситуациями. Так как все, что окружает нас, имеет отношение к геометрии. Ничто вокруг не может остаться незамеченным под ее пристальным взглядом. Геометрия помогает человеку идти по миру с широко открытыми глазами, учит его внимательно смотреть вокруг и замечать красоту обычных вещей, смотреть и думать, думать и делать выводы.
На уроке мы рассмотрим красивые задачи, решить которые вам помогут знания, полученные вами при изучении темы «Подобие треугольников».
Ученики записывают в тетради дату и тему урока.
Актуализация опорных знаний
Перед большой работой выполним «Разминку». Здесь учитывается ваша активность:
Закончите утверждение:
а) Если два угла одного треугольника соответственно равны… (двум углам другого, то такие треугольники подобны).
б) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы… (заключенные между этими сторонами, равны, то такие треугольники подобны).
в) Если три стороны одного треугольника пропорциональны… (трем сторонам другого треугольника, то такие треугольники подобны)
г) Биссектриса треугольника делит противолежащую сторону на… (отрезки, пропорциональные прилежащим сторонам)
д) Отношение периметров подобных треугольников равно… (коэффициенту их подобия)
е) Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное…(для отрезков, на которые делится гипотенуза это высотой.)
ж) Катет прямоугольного треугольника, есть среднее пропорциональное… (для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла)
з) Если через точку внутри окружности провести хорды, то … (произведение отрезков хорды есть величина постоянная)
–Могут ли быть подобными прямоугольный и равнобедренный треугольники? Почему?
– Верно ли, что подобные треугольники могут быть равными?
– Верно ли, что у подобных треугольников углы соответственно равны?
(Верно ответившие получают балл в колонку “теория” листа контроля.)
Устные упражнения.
Составить ключевое слово из букв правильных ответов к задачам:
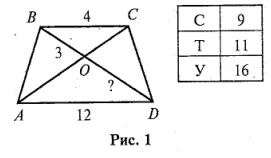
Задача 1.
ABCD – трапеция. (рис. 1)
Найдите OD.
З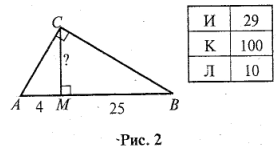
адача 2.
СМ – высота, АМ = 4, ВМ = 25. (рис. 2)
Найдите СМ.
З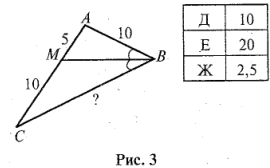
адача 3.
ВМ – биссектриса треугольника АВС. (рис. 3)
Найдите СВ.
З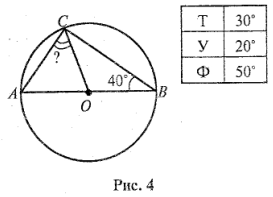
адача 4.
Найдите угол АСО. (рис. 4)
З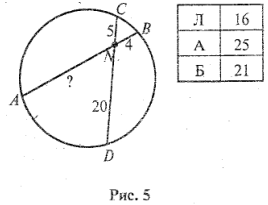
адача 5.
Найдите AN. (рис. 5)
Какое слово зашифровано? Ответ: Фалес
Измерение на местности
Самый древний способ измерения высоты пирамиды.
Я хочу прочитать вам маленькую притчу.
“Усталый пришел северный чужеземец в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона, что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы.
— Кто ты? — спросил верховный жрец?
— Зовут меня Фалес. Родом я из Милета.
Жрец надменно продолжал:
— Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? — жрецы согнулись от хохота. — Будет хорошо, — насмешливо продолжал жрец, — если ты ошибешься не более, чем на сто локтей.
— Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.
Лица жрецов потемнели. Какая наглость! Этот чужестранец утверждает, что может вычислить то, чего не могут они — жрецы Великого Египта.
— Хорошо, сказал фараон. — Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим твое искусство”.
Фалес нашел решение этой задачи. Он воткнул палку вертикально в землю и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды».
Задача. Измерение высоты пирамиды. (рис. 11)
А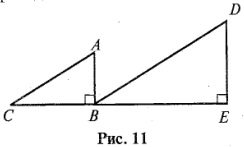
В = 4локтя, ВС = 6 локтей, ВЕ = 200 локтей.
Найдите высоту пирамиды.
З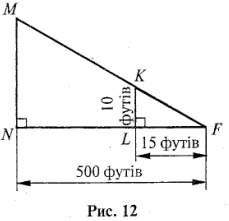
адача. Измерение высоты скалы героями Жюля Верна.
Найдите высоту MN скалы (рис. 12)
Работа в группах
З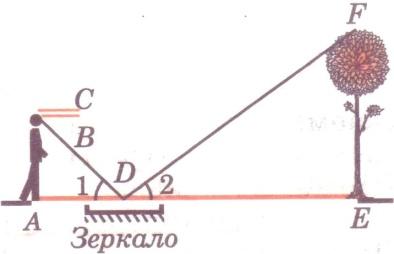
адача 1.
Для определения высоты дерева можно использовать зеркало так, как показано на рисунке. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека (точку В). Определите высоту дерева, если АС = 165 см, ВС = 12 см, АD = 120 см, DE = 4,8 м, 1 = 2.
З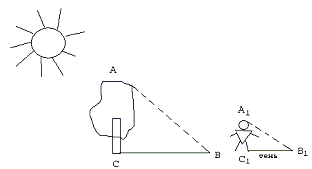
адача 2.
Длина тени дерева 21 м. В это же время суток тень человека ростом 1,8 м составляет 2,7 м. Какова высота дерева?
З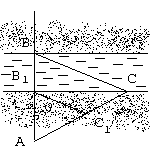
адача 3.
На рисунке показано, как можно определить ширину BB1 реки, рассматривая два подобных треугольника ABC и A1B1C1. Определите BB1, если AC = 100 м, AC1 = 32 м, AB1 = 34 м.
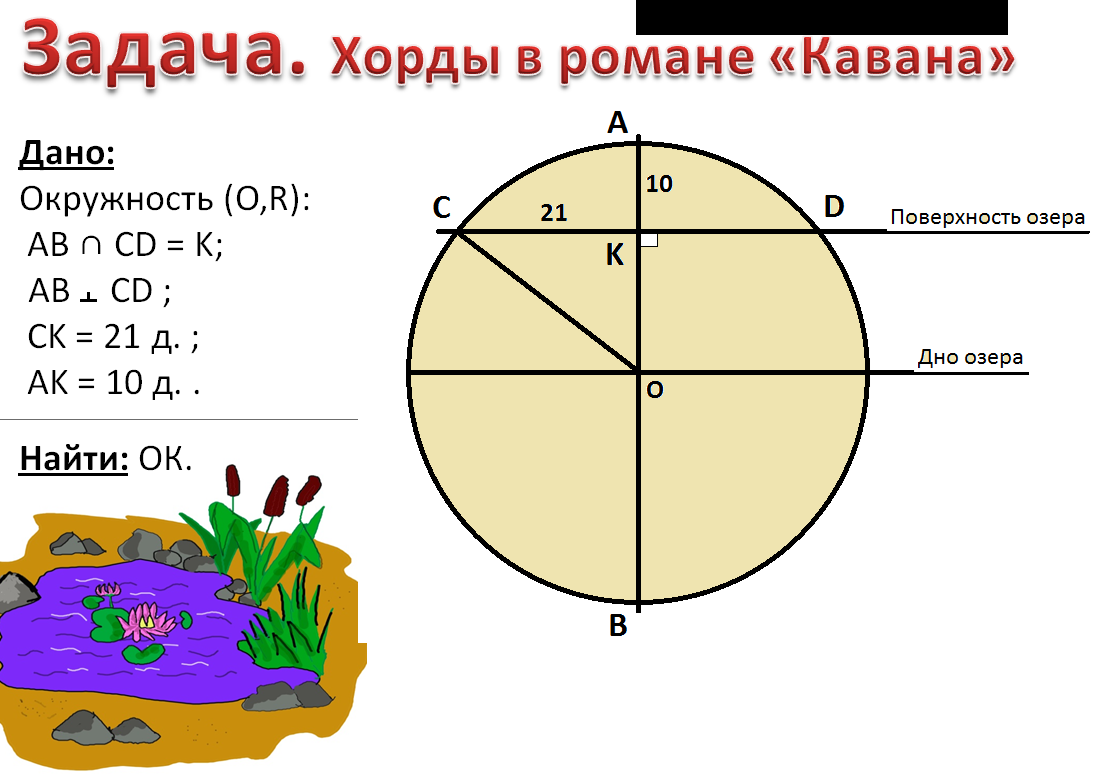
«Лилия на одну пядь поднимавшаяся над поверхностью воды, под порывом свежего ветра коснулась поверхности озера в 21 дюйме от прежнего места; исходя из этого требовалось определить глубину озера.»
Домашнее задание
Задача
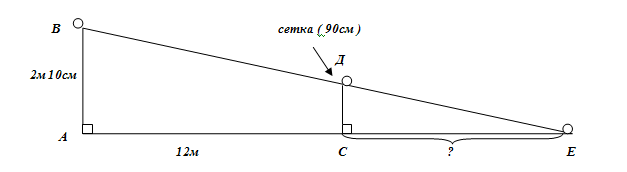
Теннисный мяч подан с высоты 2м 10см и пролетел над самой сеткой, высота которой составляет 90см. На каком расстоянии от сетки мяч ударится о землю, если он подан от черты, находящейся в 12м от сетки, и летит по прямой? 
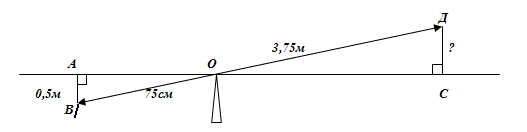
Задача
Короткое плечо шлагбаума имеет длину 75 см, а длинное плечо — 3,75м. На какую высоту поднимается конец длинного плеча, когда конец короткого опускается на 0,5м?
3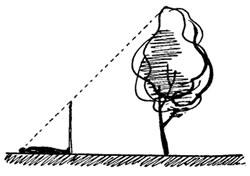
. По шесту. Взять шест, равный своему росту, и установить его на таком расстоянии от предмета (дерева), чтобы лёжа можно было видеть верхушку дерева на одной прямой с верхней точкой шеста.
Высота дерева будет равна расстоянию от головы наблюдателя до основания дерева.
Подведение итогов оценивания учащихся.
Скажи мне – и я забуду.
Покажи мне – и я запомню.
Вовлеки меня – и я научусь.
Китайская пословица
Меры длины:
1 локоть =46см
1 фут =30см
1 пядь =25см
1 дюйм =2.5см
